The project
For several years now I've tried to combine my programming self with my maths teacher alter ego by working on a symbolic calculator that would show the substeps of the manipulations made, to allow people to more easily understand the intricacies of algebra. Now I'm finally finished, and I am ever so happy to present to you - Algebra Explorer!
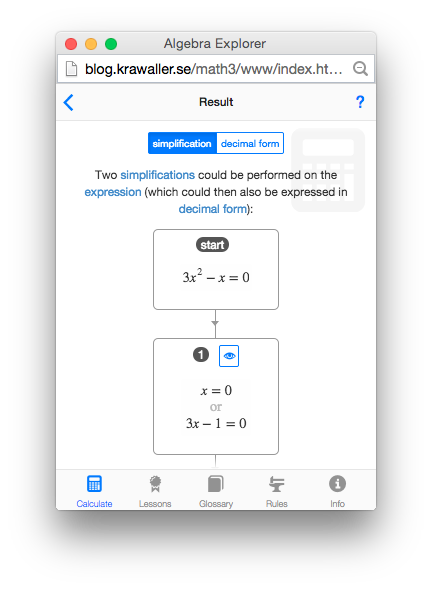
You can find out more by visiting the homepage, but as it is a web app you can also try it out right here by clicking the button below!
This post won't talk too much about the pedagogical side or the app functionality, but instead relate how the app was built.
Payment model
After trying out some different approaches I decided to make the app freely available online, and charge for an iOS version (Android planned too, but so far I haven't managed to bring myself to fix that). Since the online version works fine in a mobile browser too the app really isn't necessary, but useful if you want an offline version or just want to support the project.
Time will tell if this model is at all viable, but at this point I'm not too bothered by revenue - I'll never ever get back what my spent unpaid time is worth anyway. And also it seemed like a nice way to leverage the power of the web stack.
Tech stack
As I have been toiling away at this project for years and years and years (I remember sketching out the prototype on the whiteboard of the school in Blacklake prison in 2007), the choices regarding building blocks are not what present day David would make. But, here we go:
- CoffeeScript: Yeah, I know, I'm sorry. When I started (this version of the codebase) CS was all the craze, and I had my seat on the train. But I must say, diving down that rabbit hole definitely made me a stronger JS programmer!
- Backbone: Maybe not that bad of a fit, as my needs were rather specific and Backbone gave me lots of freedom.
- Vows: I'll talk some more about the unit testing towards the end of this post.
- Mathjax: For displaying mathematics in browsers without native support for MathML.
- Cordova: Initially I used the phonegap build service, but their repo size limit and other weirdness made me eventually install Cordova locally instead.
Other than that, I built everything myself. This was more ignorance than pride; for example, had I known more about parsing theory I would have used a library as a foundation for my own instead of doing everything from scratch.
Algebraic representation
First off I designed my own data format for mathematics. It is very simple; everything expression has a type, some have a val and some have objs (meaning children). Here is a regular number:
{
"type": "number",
"val": 7
}Here is the sum x+pi/(4^3):
{
"type": "sum",
"objs": [
{
"type": "variable",
"val": "x"
},
{
"type": "fraction",
"objs": [
{
"type": "constant",
"val": "pi"
},
{
"type": "power",
"objs": [
{
"type": "number",
"val": 4
},
{
"type": "number",
"val": 3
}
]
}
]
}
]
}Substeps under the hood
The main pedagogical idea behind the app was to show substeps of everything, and not sweeping anything under the rug. Complex rules should break down into a small set of basic truths. I used this same approach under the hood; the basic truths, which I call atomic operations, all return a maths expression, while composite operations explicitly use other operations.
For example, consider the basic truth that we can always remove an exponent 1 from a power. No matter what the value of the base is, an exponent of 1 can be removed. Here is the source code for this atomic operation:
oneExpPowerToBase = # x^1 = x
info:
name: "oneExpPowerToBase"
effect: "simplifying"
opposite: "raiseByOne"
example: "x^1"
tags: ["exponentiation","power","number1","remove","neutralelement"]
lesson: "power101"
prints:
errors: ["expmustbeone"]
target:
type: "power"
validate: ({deps,target:objs:[base,exp]})-> if not deps.equal exp, one then Err "expmustbeone", [1] else OK
perform: ({target})->
result: target.objs[0]
beforemarks: [[1]]Note how the result when calling perform will be target.objs[0]. Since the target of the operation is always a power, what is returned is the first child of the power, namely the base. And of course this is what remains if we "remove" the exponent.
Now consider the rule that if a power has an exponent of 0, it is equal to 1 (actually it is not quite that simple since the base cannot be 0 too, but never mind that for now). This is not a basic truth, but a consequence of the above rule and several other rules. Here's what this looks like in the app:
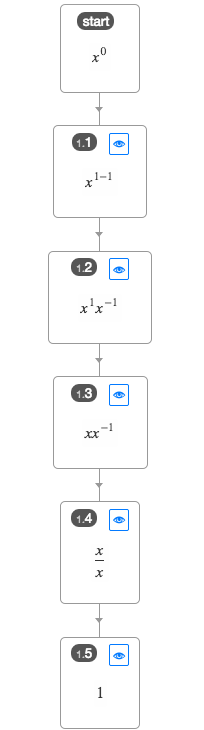
And here is the source code for this operation, where you can see it explicitly calling each substep:
zeroExpPowerToOne = # x^0 = 1
info:
name: "zeroExpPowerToOne"
effect: "simplifying"
example: "x^0"
uses: ["numToSum","biSumExpPowToProd","oneExpPowerToBase","negExpFacProdToFrac","sameNumerDenomFracToOne"]
tags: ["exponentiation","number1","number0","power","collapse","neutralelement"]
opposite: "oneToZeroExpPower"
lesson: "powernegexp"
prints:
errors: ["expmustbezero"]
target:
type: "power"
validate: ({deps,target:objs:[base,exp]})-> if not deps.equal exp, zero then Err "expmustbezero", [1] else OK
perform: (o)->
o.do "numToSum","turnzeroexpto1minus1",aim:[1],argument: Sum one,Neg one
o.do "biSumExpPowToProd","splitpow"
o.do "oneExpPowerToBase","dropexp1",aim:[0]
o.do "negExpFacProdToFrac","movetodenom",selection:[[1]]
o.do "sameNumerDenomFracToOne","andcollapsefracto1"
o.beforemark [[1]]Modelling the code this way made it easier for me to show the substeps for the user, as the end result of a simplify call will be a nested object with each step info retained. Thus I can allow the UI to dig however deep the user wishes.
Localization
Probably you've already gleaned that the app is bilingual. I manage localization through a simple literal system. For example, here's the text content to go with the above operation:
zeroExpPowerToOne:
id: 2
sv:
name: "omvandla potens till 1"
explanation: "Exponenten berättar hur många gånger vi multiplicerar basen med sig själv. Men har vi 0 faktorer så återstår bara det neutrala elementet för multiplikation, nämligen 1."
targets: "en potens med exponent 0 och bas skiljd från 0"
returns: "det naturliga talet 1"
effect: "Detta är en förenklande regel, eftersom den kollapsar potensen till talet 1"
steps:
turnzeroexpto1minus1: "Först delar vi upp exponenten 0 i en summa, för att sedan kunna dela upp potensen."
splitpow: "Vi delar upp potensen i två potensfaktorer. De nya potenserna får exponenterna 1 och -1."
dropexp1: "Exponenten 1 tar vi bort."
movetodenom: "Den andra potensen flyttar vi ner i nämnaren, vilket gör att exponenten byter tecken, blir 1 och försvinner!"
andcollapsefracto1: "Nu har vi ett bråk med identisk täljare och nämnare, vilket vi kollapsar till 1!"
en:
name: "transform power to 1"
explanation: "The exponent tells us how many times we multiply the base with itself. But if we have 0 factors we just get the neutral element of multiplication, namely 1."
targets: "a power with exponent 0 and base not equal to 0"
returns: "the natural number 1"
effect: "This is a simplifying rule, since it collapses the power to the number 1"
steps:
turnzeroexpto1minus1: "First we split the exponent 0 into a sum, which will enable us to split the power."
splitpow: "Now we split the power into two power factors. The new powers get the exponents 1 and -1."
dropexp1: "The exponent 1 can be removed."
movetodenom: "The other power we move into the denominator, which makes the exponent become 1 and disappear."
andcollapsefracto1: "Now we have a fraction with identical numerator and denominator, which we can collapse to 1!"Note how the steps keys correspond to the strings used in the zeroExpPowerToOne source.
Initially I was worried about keeping such large objects in memory - the one defined in this file, containing all operation descriptions and substep explanations, is over half a megabyte! But as it turned out, this proved to work rather smoothly even on lower end devices.
Regular expressions ftw
As you can see in the screenshot up top, some terms inside explanations are clickable. Algebra Explorer has an integrated glossary - click the term to navigate to the definition for that term. This is done dynamically by defining a matcher for each glossary entry. Here's the definition for the word extract:
extract:
matcher:
en: "extracte?d?i?n?g?"
sv: "br[yö]ta?e?r?s?( vi)? ut"
headline:
en: "extract"
sv: "bryta ut"
description:
en: "When we factorise an expression because we are interested in one of the resulting factors, we say that we extracted that factor."
sv: "Om vi faktoriserar ett uttryck för att vi är intresserade av en av de resulterande faktorerna, så säger vi att vi har brytit ut (eller 'extraherat') den faktorn."This saved me from manually having to write the links, which would have made authoring the texts a real drag.
At first this didn't work too well - sometimes there was a wording I hadn't anticipated and the word wouldn't be clickable, and other times words would be made clickable when they shouldn't be as they meant something entirely different in that context. This got better over time as I got better at phrasing dexterous but still picky regexes.
I also made a special MAKESAFE matcher which wraps all matched content in a span, to prevent it from later being made clickable. This matcher used to be very complicated as it had to cater for lots of false positives, but now this is all that remains:
MAKESAFE:
matcher:
en: "introduced to|[01]\\.[0-9]+|number of times|any number of|the number of|a number of|1\\/|E?e?ven (though|if the)|introduced logic"
sv: "vardagligt tal|introduceras till|[01][\\,\\.][0-9]+|1\\/|introducerade logik"Unit testing with Vows
For unit testing my choice fell on Vows, which turned out to be a very good fit. The main advantage for me was that the test definitions in vows are object literals, which makes it easy to write helper functions (they call them "macros") to clean up your tests.
Here is what it can look like, using the mergeSameBaseFacs operation as an example:
tests.addBatch "the mergeSameBaseFacs op":
topic: -> tools.mergeSameBaseFacs
hasInfo: info
name: "mergeSameBaseFacs"
effect: "simplifying"
example: (str:"x*y*x2",selection:[[0,2]])
"the target def says product": targetIs "product"
"the selection def": selection
"has min 2": min 2
"the auto func": auto
"for no same base fac prod": test
withTarget: (Product x, z, Power y,two)
"we get err": isError "musthavesamebasefacs"
"for same base fac prod": test
withTarget: (Product x, z, two, Power x,two)
"we get correct obj": isObj
selection: [[0,3]]
"when neg hiding same": test
withTarget: (Product x, z, two, Neg Power x,two)
"we get correct obj": isObj
selection: [[0,3]]
"the perform func": perform
"when leftover facs": test
withTarget: (Product x, z, (Power x,three), Power x,two)
withSelection: [[0,2,3]]
"we get right answer": resultIs (Product (Power x, Num 6), z)
"sels are beforemarked": beforemarks [[0],[2],[3]]
"pow is aftermarked": aftermarks [[0]]
"when no leftovers": test
withTarget: (Product x, (Power x,three), Power x,two)
withSelection: [[0,1,2]]
"we get right answer": (resultIs Power x, Num 6)
"and no aftermarks": aftermarks undefined
"when non-numeric": test
withTarget: (Product x, Power x, y)
withSelection: [[0,1]]
"we get right answer": (resultIs Power x, Sum one, y)
"when multinonnumeric": test
withTarget: (Product (Power two, x), (Power two, y), Power two, z)
withSelection: [[0,1,2]]
"we get right ans": (resultIs Power two, Sum x,y,z)
"when partly numeric": test
withTarget: (Product (Power two, three), (Power two, y), two)
withSelection: [[0,1,2]]
"we get right ans": (resultIs Power two,Sum (Num 4), y)
"when one negation": test
withTarget: (Product (Power two, three), (Neg Power two, y), two)
withSelection: [[0,1,2]]
"we get right ans": (resultIs Neg Power two,Sum (Num 4), y)Combined with the added readability of CoffeeScript, this really makes for some sleek tests!
Wrapping up
When I started, part of my motivation was to show that it was possible to build this kind of thing with JavaScript. That's not a point that needs to be made anymore, and there are already several other CAS implementations built on the web stack.
Still, I am rather proud of my creation! Sure, it contains many rough edges, the UI isn't that intuitive, and many times the fact that this is a one man show shines through. But for those who get over the initial threshold it seems the app can really help them grokk algebra. We're starting now to roll it out for the maths students in the Swedish prisons, and I hope teachers outside the walls will catch on too. Time will tell.
And also the code is really pretty. :)
Anyhow, if you have an interest then please do give Algebra Explorer a spin! Any and all feedback much appreciated!